E je eliptička krivulja nad
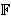
 ,
a P je točka prostog reda n na
E(
,
a P je točka prostog reda n na
E(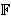
 ).
Svaki korisnik napravi sljedeće:
).
Svaki korisnik napravi sljedeće:
Korištenje originalne poruke u generiranju digitalnog potpisa često rezultira vrlo dugačkim potpisom. Stoga se umjesto originalne poruke često koristi "sažetak poruke" (message digest) koji se dobije primjenom neke hash funkcije. U kriptografiji, hash funkcija je jednosmjerna funkcija koja za ulazni podatak proizvoljne duljine daje izlazni podatak fiksne duljine. Među najpoznatije hash funkcije spadaju MD5 (output od 128 bitova), RIPEMD-160 (output od 160 bitova) i SHA-1 (output od 160 bitova).
Neki kriptosustavi s javnim ključem (npr. RSA) mogu se direktno iskoristiti za potpisivanje poruke. Ipak, najpoznatije metode za generiranje digitalnih potpisa su Digital Signature Algorithm (DSA/DSS) i Elliptic Curve Digital Signature Algorithm (ECDSA). DSA je zasnovan na problemu diskretnog logaritma u multiplikativnoj grupi konačnog polja, dok ECDSA predstavlja njegov analogon i koristi eliptičke krivulje. U siječnju 1999. ECDSA je prihvaćen kao ANSI standard.
Opisat ćemo tri etape od ECDSA.
1. ECDSA generiranje ključeva.
E je eliptička krivulja nad
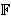
 ,
a P je točka prostog reda n na
E(
,
a P je točka prostog reda n na
E(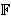
 ).
Svaki korisnik napravi sljedeće:
).
Svaki korisnik napravi sljedeće:
a) Izabere slučajan broj d iz skupa {1, ... , n - 1};2. ECDSA generiranje potpisa.
b) Izračuna Q = [d] P;
c) Q je javni, a d tajni ključ.
a) Izabere slučajan broj k iz skupa {1, ... , n - 1};3. ECDSA provjera potpisa.
b) Izračuna [k] P = (x1, y1) i r = x1 mod n. Ako je r = 0, onda se vrati na korak a);
c) Izračuna k-1 mod n;
d) Izračuna s = k-1(H(m) + dr) mod n, gdje je H hash funkcija. Ako je s = 0, onda se vrati na korak a);
e) Potpis poruke m je uređeni par prirodnih brojeva (r, s).
a) Dobiti Alicein javni ključ Q;Uvjet r
b) Provjeriti da su r i s cijeli brojevi iz skupa {1, ... , n - 1};
c) Izračunati w = s-1 mod n i H(m);
d) Izračunati u1 = H(m)w mod n i u2 = rw mod n;
e) Izračunati [u1] P + [u2] Q = (x0, y0) i v = x0 mod n;
f) Prihvatiti potpis kao vjerodostojan ako i samo ako je v = r.
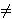 0
osigurava da se u potpisivanju stvarno koristi Alicein tajni
ključ d, dok se uvjet s
0
osigurava da se u potpisivanju stvarno koristi Alicein tajni
ključ d, dok se uvjet s
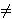 0 pojavljuje zbog
koraka 3.c).
0 pojavljuje zbog
koraka 3.c).
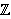 199 zadana
je jednadžbom
y2 =
x3 + x + 3.
Dokažite da je
E(
199 zadana
je jednadžbom
y2 =
x3 + x + 3.
Dokažite da je
E(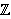 199)
ciklička grupa s n = 197 elemenata
i generatorom P = (1,76).
199)
ciklička grupa s n = 197 elemenata
i generatorom P = (1,76).
| Web stranica seminara | Andrej Dujella - osobna stranica |